Simulations with precise spike times
The simulation resolution h and the minimum synaptic transmission delay dmin define the two major time intervals of the scheduling and simulation flow of NEST: neurons update their state variables in steps of h, whereas spikes are communicated and delivered to their targets in steps of dmin, where dmin is a multiple of h.
Traditionally, spikes are constrained to the simulation grid such that neurons can propagate their state variables for an entire h-step without interruption by incoming spikes. This enables faster simulations of neurons with linear sub-threshold dynamics as a precomputed propagator matrix for a time step of fixed size h can be employed (Rotter & Diesmann, 1999).
Neurons buffer the incoming spikes until they become due, where spikes can be lumped together provided that the corresponding synapses have the same post-synaptic dynamics. Within a dmin-interval, each neuron independently proceeds in steps of h: it retrieves the inputs that are due in the current time step from its spike buffers and updates its state variables such as the membrane potential.
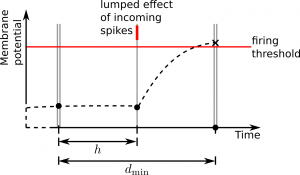 Propagation of membrane potential in case of grid-constrained spiking. Filled dots indicate update of membrane potential; black cross indicates detection of threshold crossing. As visual guidance, dashed black curves indicate time course of membrane potential. For simplicity, dmin=2h.
Propagation of membrane potential in case of grid-constrained spiking. Filled dots indicate update of membrane potential; black cross indicates detection of threshold crossing. As visual guidance, dashed black curves indicate time course of membrane potential. For simplicity, dmin=2h.
If after an update the membrane potential is above the firing threshold, the neuron emits a spike and resets its membrane potential. Due to time discretization both spike and reset happen at the right border of the h-step in which the threshold crossing occurred; the spike is time stamped accordingly.
NEST enables also simulations with precise spike times, which are represented by an integer time stamp and a double precision offset. As the incoming spikes divide the h-steps into substeps, a neuron needs to update its state variables for each substep.
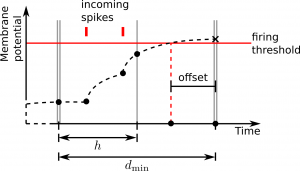 Propagation of membrane potential in case of off-grid spiking. Dashed red line indicates precise time of threshold crossing.
Propagation of membrane potential in case of off-grid spiking. Dashed red line indicates precise time of threshold crossing.
If after an update the membrane potential is above the firing threshold, the neuron determines the precise offset of the outgoing spike with respect to the next point on the time grid. This grid point marks the spike's time stamp. The neuron then emits the spike and resets its membrane potential.
Models with precise spike times in NEST
poisson_generator_ps creates Poissonian spike trains, where spike times have an integer time stamp and a double precision offset. It is hence dedicated to simulations with precise spike times. The device can also be connected to grid-constrained neuron models, which only use the time stamps of the spikes and ignore their offsets. However, spike generation with poisson_generator_ps is less efficient than with its grid-constrained counterpart poisson_generator.
parrot_neuron_ps repeats the incoming spikes just as its grid-constrained counterpart parrot_neuron but it is able to represent precise spike times.
iaf_psc_delta_canon is an integrate-and-fire neuron model with delta-shaped post-synaptic currents that employs precise spike times; its grid-constrained counterpart is iaf_psc_delta. In this model the precise location of an outgoing spike is determined analytically.
iaf_psc_alpha_canon and iaf_psc_alpha_presc are integrate-and-fire neuron models with alpha-shaped post-synaptic currents that employ precise spike times; their grid-constrained counterpart is iaf_psc_alpha. The neuron models have been developed in the context of Morrison et al. (2007). As both models employ interpolation in order to determine the precise location of an outgoing spike, the achieved precision depends on the simulation resolution h. The models differ in the way they process incoming spikes, which also affects the attained precision (see Morrison et al. (2007) for details).
iaf_psc_exp_ps is an integrate-and-fire neuron model with exponentially shaped post-synaptic currents that employs precise spike times; its grid-constrained counterpart is iaf_psc_exp. It has been developed in the context of Hanuschkin et al. (2010), which is a continuation of the work presented in Morrison et al. (2007). As the neuron model employs an iterative search in order to determine the precise location of an outgoing spike, the achieved precision does not depend on the simulation resolution h. The model can also be used through the PyNN interface.
The source code of these models is in the precise module of NEST.
Questions and answers about precise neurons
During the review process of the above mentioned papers, we came up with a list of questions and answers pertaining to the implementation and usage of precise spiking neurons. This list can be found here.
